光で組み合わせ最適化問題を解く「量子ニューラルネットワーク」とは?:5分で分かる最新キーワード解説(3/4 ページ)
量子ニューラルネットワーク実験結果と将来
この仕組みを用いた実験では、「Max cut問題」と呼ばれるグラフ問題が解かれた。これは「NP困難問題」と呼ばれる数学的な問題の1つである。多くの点(ノード)が線(エッジ)で互いに結ばれている状態を考え、点を2つの集まり(部分集合)に分けるときに、線を切る数が最大となる分け方を求めるという問題である。
1つの実験はノード数2000、エッジ数19990(結合密度1%)のケースで行われた。近似解であるが、わずか5ミリ秒で13313カット数で分けることができた。図5に示す(a)が問題で、ピンクの点がノード、よく分からないほど複雑な綿毛のように見える白い線がエッジである。
処理の結果が(b)で、ピンクの点が赤の点と青の点(それぞれ部分集合)に分けられた。切られたエッジが緑色で表されている。どれだけ高速かがイメージできるだろう。
またノード数2000、エッジ数1999000(結合密度100%)の完全グラフ問題では、一般的に十分な精度(イジングエネルギーがマイナス6万レベル)までの計算を行うのに、70マイクロ秒しかかからなかった。同じ計算を専門家によって最高レベルにチューニングされたデジタルコンピュータで行ったところ、最短で3.2ミリ秒であった。比較すると約50倍の高速化ができたことになる。
またグラフ問題で100ノードあると解の全候補は2の100乗(10の30乗、1000兆の1000兆倍)に及ぶが、その厳密解を求める実験も行われ、5ミリ秒以内で成功確率20%で正解できている。
これまでの他技術と比較しての特徴は、ノード当たりのエッジ数が多い場合に圧倒的に優れた処理能力があるところだ。例えばD-Wave IIXではノード数は1152、ノード当たりエッジ数は最大6、無向グラフの場合のエッジ総数3360、解ける完全グラフのサイズは15以下であるのに対し、本技術はノード数2048、ノード当たりエッジ数最大2047、無向グラフの場合のエッジ総数209万6128、解ける完全グラフサイズは2048となっている。これは、より柔軟に組合せ最適化問題を処理対象にできることを意味している。
NTTの武居氏は、今後OPOの数のさらなる上乗せを目指すとし、3年後には2万5000個にまで増やす考えだ。理論的には100万個まで増やすことができるが、あまり多くすると不安定になるという。人間の脳のニューロンは1000億個といわれているのでそれには及ばないが、OPOが増えるほど対象にできる案件が増えそうだ。
また、アプリケーションもさまざまに考えられる。例えば、創薬では化合物の結合のパターンで適切な組合せ候補をリストアップすることができよう。無線通信システムでは、チャネルの最適化に応用できそうだ。さらに天体望遠鏡や監視カメラなどの映像が不鮮明であっても、画像処理によって正確な情報再現ができるようになるかもしれない。
なお、ゆくゆくは外部からも量子ニューラルネットワークをインターネットを介して利用できるサービスを開始する計画もあるとのことだ。NTTの実機と、NIIの量子シミュレーションサービスの組み合わせが希望者に提供されることになりそうだ。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
製品カタログや技術資料、導入事例など、IT導入の課題解決に役立つ資料を簡単に入手できます。
- リチウムイオン電池も終了か 40年眠っていた、充電を爆速化する「古くて新しい電池」って?:866th Lap
- AIに書かせたコードはどこが「危ない」? プロがガチ採点して分かったこと
- 「国家資格で食える」はもう古い? 5年分の調査で見る、AWS、セキュリティに続く“次の資格”
- AIアプリ開発「Dify」って結局何がすごいの? 機能、料金、ユースケースを徹底解説
- 正規認証が悪用される? Microsoft 365の権限を奪う「デバイスコードフィッシング」とは
- 会社の規則は穴だらけ? 誰も守ってくれない「無視されるITルール」【実態調査】
- PC高騰、いつまで続く? IDCアナリストに聞く値上げ時代の賢いPC調達術
- 「AI時代に“御社の強み”は通用しますか?」 8割のSIerが漏らした“まさかのホンネ”【調査】
- 「Geminiを使えばPowerShellの習得も楽勝」のはずだったが……:850th Lap
- ランサムウェア対策、何から始める? 悩める中小企業を救うIPAの"神ツール"
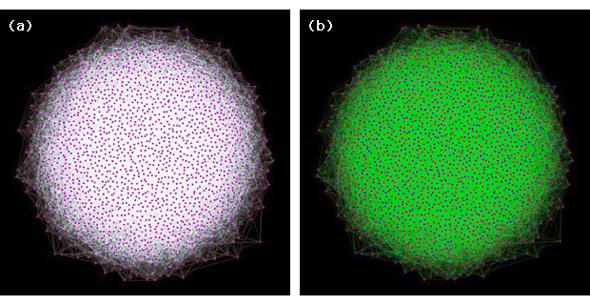 図5 Max cut問題の近似解のビジュアル表現(出典:NTT)
図5 Max cut問題の近似解のビジュアル表現(出典:NTT)